I spent a while this summer reading math books and popular science, trying to figure out what a life in "research" might look like; in late Spring I began to sense that it was time to wake up my brain and start thinking again, and the best way forward seemed to be to find examples of lives-well-lived in science and study the cases.
I'm so glad I found "The Second Kind of Impossible: the Extraordinary Quest for a New Form of Matter" by Paul Steinhardt. The book is a trip report of Paul's decades-long relationship with a peculiar type of matter called a "quasicrystal". I'll give a short summary, then discuss what struck me as so wonderful about the book, and finish out by including my more detailed notes in case you want to dig deeper.
Summary
Paul is, I guess, best known for coming up with the inflationary theory of the universe in the early 80s; I would have imagined that that topic would be consuming. Shows what I know. Paul spent the summer of 1980 working on a computer simulation of what happens when you rapidly cool a liquid down to a frozen state.
A liquid is a random arrangement of atoms, all jostling around past each other. If you cool a liquid slowly, the atoms will begin to clump together into a solid; imagine water freezing into ice as an example. If you cool slowly enough the resulting solid will assume a form called a "periodic crystal". The water molecules in ice stack "together like oranges on display at a grocery store. The structure - technically called face-centered cubic - has the same symmetry as a cube, consistent with all the known rules of crystallography." (Steinhardt, Loc 358)
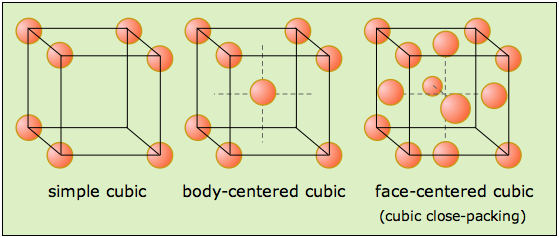
This arrangement is called a periodic crystal because the pattern, the cube, in this case, repeats itself as you scan through the solid. It turns out that there are only 230 possible periodic crystal structures in 3 dimensions. Any crystal you find in nature will have one of these shapes.
What would happen if you cooled water so fast that the molecules didn't have time to arrange themselves into a periodic crystal? Maybe some mix of randomness and order, Paul guessed. What he found, instead, was a "forbidden symmetry" - a crystal that somehow had the symmetry of a 12-sided die, an icosahedron, which is not one of the shapes allowed for a periodic crystal.
Of course, there is nothing wrong with having a single tile in the shape of a regular pentagon. You can make a single tile any shape you wish. But it is impossible to cover a floor with regular pentagons without leaving gaps. The same applies to an icosahedron. It is possible to make a single three-dimensional die in the shape of an icosahedron. But you cannot fill space with icosahedrons without leaving gaps and holes. (Steinhardt, Loc 408)
This discovery kicked off an incredible, decades-long quest to figure out what the hell is going on. Paul got a grad student, Dov Levine, interested in the problem of "quasicrystals", arrangements of matter that weren't periodic crystals... but still showed inexplicable signs of order.
The book is full of wonderful references, scientific celebrity appearances and little knowledge nuggets that could keep you busy on their own for months. For example, the duo gets their first clue about what's going on when Dov discovers Roger Penrose's "Penrose tilings", arrangements of tiles that never repeat, even on infinite planes. This is straight out of the puzzling world that my dad, Bill Ritchie, is a big part of; Martin Gardner, my dad's hero, wrote a book about these tilings called "Penrose Tiles to Trapdoor Ciphers".
Richard Feynman (Paul's mentor!) makes an early appearance and encourages Paul to keep poking at this problem seemingly unrelated to the inflationary theory that's making Paul famous:
My main scientific interests were pointing elsewhere at the time. But I took advantage of the summer research opportunities because I was intrigued by the fact that the atomic arrangement of something as rudimentary as amorphous matter was not yet known. In that, I was intentionally following one of the most important lessons learned from my mentor, Richard Feynman: It is wise to follow your heart and seek out good problems wherever they may lead, even if it is not in the direction you thought you were supposed to be headed. (Steinhardt, Loc 384)
Paul and Dov build on Penrose's work and generate an entire theory of 3d quasicrystals, or arrangements of matter that have symmetry, but never actually repeat. No one had ever seen anything like this in nature... until a massive coincidence occurs and, without knowing about Paul and Dov's work, someone finds one of these things while investigating different aluminum alloys in the lab.
The book tracks the story of the theory, the coincidences, and then Paul's later obsession with the next obvious idea - can these quasicrystals form in nature? Has anyone ever found one in the wild?
The answer turns out to be yes, and leads Paul deep into geology, and finally on an expedition that into the Russian interior on a quest to find quasicrystals that seem to have arrived from space.
Come on. How much more awesome can it get?
Thoughts
I've been writing many trip reports of late, and this whole book is a trip report of a legendary physical and intellectual adventure. It's a celebratory book, meant to get you excited about the physics that Paul is tackling, and the pleasure that can come from taking a passing curiosity seriously and trying to track down the answer.
It's easy to imagine passing over the initial curiosity of a strange symmetry popping up in a computer simulation. Paul keeps at it for years with no indication that the things he's simulating are even possible in the physical universe, with the collection of elements we have on earth. He's rewarded with the discovery of an entirely new kind of matter that actually does exist in nature.
Can you imagine making up, and then discovering, a whole new class of matter, like the metals?
There is a sense of suspense throughout! Paul and his collaborators spend their time learning the recreational math of Penrose tiles, tracking down geology samples, analyzing tiny little pieces of rock with no backup... and doors keep opening onto the next phase of the problem, often after months or years with no result.
The intuition that Paul ended up developing was outrageous. There are multiple moments in the book where Paul and the geologists he's working with are able to immediately identify some x-ray image of crystal structure as coming from some particular meteorite, some famous sample, just based on the rare geometric arrangement that the x-rays create on photo paper after scattering through the rock. Geology is not technically Paul's "field"... but maybe the grouping of knowledge into fields is arbitrary, and not helpful when you're following a problem around.
Should you read this book?
Yes, I think so if you have any interest in science; This is a great book about scientific discovery, and how a problem can fractally unfold and stay interesting through so many levels.
I don't know if this is what being a typical professor is like, really. Paul doesn't discuss his non-academic life, or family, or teaching; it's not really a memoir. Paul comes across as a humble, grateful dude, just happy to have the chance to get to peek behind the curtain.
More Detail
I have so many notes that I can't bear to delete, so here's a brain dump on the book itself, and various topics that pop up.
Quasicrystals
You can also get stoked about quasicrystals! I don't know if you can learn a ton here, but if you want to step off and learn more about the various topics, I can offer some suggestions. If you read this book slowly and absorbed the examples I think the import of the various tests and mineral combinations he discusses later would be more interesting for sure.
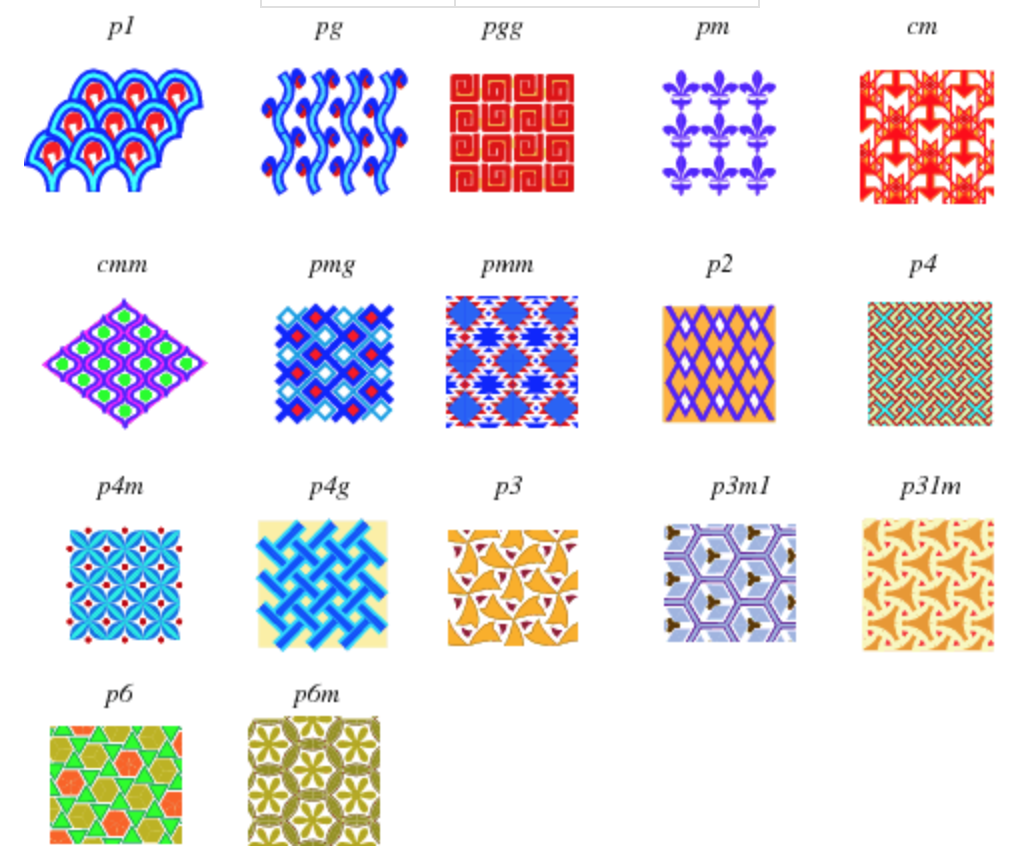
I first encountered the idea of symmetry groups in Ian Stewart's Concepts of Modern Mathematics. Chapter 7 - "Symmetry: the Group concept" - covers the mathematics and builds up to an explanation of "wallpaper groups", which is the 2-dimensional version of the mathematics behind crystallography (called "space groups" in 3 dimensions).
Just as there are 230 types of possible periodic crystals, there are 17 possible periodic arrangements on the plane, or 17 possible types of wallpaper pattern.
Aperiodic Crystals
The book covers periodic crystals and quasicrystals, which are "aperiodic"; there are in fact other kinds of aperiodic crystal, ordered arrangements of atoms with no repeating structure. One such aperiodic crystal is DNA, the molecule that encodes genetic information.
Before the actual discovery of DNA's double helix structure, the physicist Erwin Schrödinger, in 1944, had written a book called "What is Life?" (Wikipedia page) that predicted that whatever it was in living things that carried hereditary information must be some sort of highly-ordered molecule with no periodic structure. From Wikipedia:
Schrödinger explains that most physical laws on a large scale are due to chaos on a small scale. He calls this principle "order-from-disorder." As an example he mentions diffusion, which can be modeled as a highly ordered process, but which is caused by random movement of atoms or molecules. If the number of atoms is reduced, the behaviour of a system becomes more and more random. He states that life greatly depends on order and that a naïve physicist may assume that the master code of a living organism has to consist of a large number of atoms.
How naïve! Schrödinger reasoned that based on what was known about mutations and heredity, "the carrier of hereditary information [would have] to be both small in size and permanent in time"; some sort of molecule was the best known candidate.
I haven't read his book yet, but the guesses, and the philosophy he uses to come up with his theoretical model (the guiding light for Watson and Crick's search!) are fascinating.
The book "Life on the Edge: The Coming of Age of Quantum Biology" by McFadden and Al-Khalili has a chapter called "Quantum Genes" that gets into the details of how DNA encodes highly-ordered genetic data at molecular scales, where chaos usually rules and random motion wipes out any order. DNA has to actively resist that to maintain its aperiodic crystal structure.
For a more speculative discussion of DNA, check out "Cosmic Serpent: DNA and the Origins of Knowledge", by Jeremy Narby. This book might seem a bit New Age and hokey... but I recommend you read it like you'd read Paul Steinhardt's book. Narby is trying to pose a clear, well-formed question about how various cultures have extremely unlikely combinations of plant medicines; he's just not as far along in the quest as Paul, and the mist is thick around him.
Paul is a theoretical physicist from Princeton who's been engaged in a decades-long treasure hunt
What a tale! A decades-long trip report, not focused on some arbitrary athletic endeavour!
https://www.physics.princeton.edu/~steinh/
Chapter Summary
I'm including the notes I took while reading this book, for myself down the road and for you if you want a more detailed summary than the one above. Let me know if any of this is interesting in the comments, and I'll be happy to polish up any section and go into more detail.
Part I: Making The Impossible Possible
The book starts with Paul's observation (that he learned from Richard Feynman, I believe?) that there are two kinds of impossible. Some impossible things are forbidden by the laws of physics as we know them. Other impossible things are just incredibly unlikely, and very surprising. Five-fold symmetry in matter across thousands of atoms is not strictly forbidden... just incredibly unlikely. The question of why it was appearing in Paul's computer simulations is a strange and interesting one, for someone with the time to grapple with impossible things.
Paul meets Dov Levine and they decide to work on a theoretical foundation for this new kind of matter; what could be causing five-fold symmetry? They find Penrose tilings. Here's a link again to the Martin Gardner book if you want to go deeper.
The first book encodes Paul's sense of a swelling crescendo of interest and excitement and effort.
We get an encounter with Feynman! Paul gets crushed by Feynman lectures back in college. In junior year he gets the courage to ask Feynman to revive "Physics X", but for juniors and seniors.
I also learned that “impossible,” when used by Feynman, did not necessarily mean “unachievable” or “ridiculous.” Sometimes it meant, “Wow! Here is something amazing that contradicts what we would normally expect to be true. This is worth understanding!”
Then on to the history of crystallography. René Just Haüy, the "father of modern crystallography", dropping a specimen of calcareous spar and discovering crystals shaped like a rhomboid...
Woah, totally repeated! Could this be some hint about the internal structure of the building block?
These are the three building blocks:
The principles of crystallography:
The first principle is that all pure substances, such as minerals, form crystals, as long as there is enough time for the atoms and molecules to move into an orderly arrangement.
The second states that all crystals are periodic arrangements of atoms, meaning their structure is entirely composed of one of Haüy’s primitive building blocks, a single cluster of atoms that repeats over and over in any direction with equal spacing.
The third principle is that every periodic atomic arrangement can be categorized according to its symmetries, and there is a finite number of possible symmetries.
The final thing note to "periodic tilings", or wallpaper patterns in 2d. (See my description above about Quasicrystals for links to resources that talk about wallpaper patterns and symmetry groups.) In 3d there are 230 options instead of the 17 in 2 dimensions, but the basic idea is the same.
Periodic tilings are frequently used in kitchens, patios, bathrooms, and entryways. And those patterns often include one of five basic shapes: rectangles, parallelograms, triangles, squares, or hexagons.
You can't tile with pentagons, though!
Next, a discussion of tools that allow you to examine crystal symmetries in actual physical specimens.
Steinhardt and his boy, Dov Levine, start investigating. They come up with quasicrystals!
Their inspiration was Penrose tilings: https://en.wikipedia.org/wiki/Penrose_tiling
They show that if such a material existed, it would have an x-ray diffraction pattern with pentagonal symmetry... goes into what this means, etc. But it's just a theory.
How did this idea get started?
But I took advantage of the summer research opportunities because I was intrigued by the fact that the atomic arrangement of something as rudimentary as amorphous matter was not yet known. In that, I was intentionally following one of the most important lessons learned from my mentor, Richard Feynman: It is wise to follow your heart and seek out good problems wherever they may lead, even if it is not in the direction you thought you were supposed to be headed.
They find this weird forbidden symmetry in a software model that's meant to investigate this idea of a "cubatic" phase, a sort-of-periodic crystal, sort-of ordered that would appear if you rapidly cool something to solid.
An icosahedron showed up! This has 5 fold forbidden symmetry if you look down at a point.
THE SECRET
Robert Ammann, brilliant amateur... the story is getting more strange, definitely a mystery novel. They track down this guy based on based on a diffraction pattern pic posted by Martin Gardner:
They were taken directly from the work of an unknown amateur named Robert Ammann. That was the first time we had ever heard mention of the mysterious genius who communicated with very few people other than Martin Gardner, the Scientific American guru of recreational mathematicians. Mackay suggested we contact Gardner for help.
He's totally brilliant, gives them new tools to think about quasicrystal structure. Woah, then they discover the fibonacci sequence lurking! Total detective style.
And it turns out the only way to obtain a pattern of Ws and Ns that reproduces the Fibonacci numbers is to have the Ws repeat with a greater frequency than the Ns, as the Penrose tiling extends out in all directions, by a factor precisely equal to the golden ratio, an irrational number. And that is the secret of the Penrose tiling in a nutshell. A sequence composed of two elements that repeat at different frequencies, the ratio of which is an irrational number, is called quasiperiodic. A quasiperiodic sequence never repeats exactly.
OKAY, so they develop this whole theoretical model. Then, independently, Dan Schechtman, cataloguing aluminum manganese alloy properties, sees this in his lab:

Hee has no idea what's going on, sticks with it, finally publishes the results with no theoretical explanation.
Paul finds this result through another coincidence and realizes that this is experimental backup for his theoretical framework. He's a legend, right?
The experimental result starts to freak people out. Maybe there are other explanations? The x-ray pattern was a little fuzzy, after all.
They have to modify their theory with "growth" rules, since Penrose tilings at the time had to be created all at once; building them up in pieces wasn't possible. They just keep chipping away and do it, and even come up with 3d rules. It takes them 30 years to find a proof that their rules are correct. That is commitment, yikes.
Soon a scientist in Japan figures out how to make these things. Quasicrystals are real!
Part II: The Quest Begins
Okay, so they can make them in the lab. But what about in nature? Paul's main gig is physics, cosmology... he was one of the core inflationary universe inventors. Now he's deep into geology? I guess this is why it helps to get tenure.
It's now 1999, and Ken Deffeyes, a Princeton geologist, enters the story. I last encountered Ken in John McPhee's "Annals of the Former World". Ken asks Paul if anyone's ever found a natural quasicrystal.
They start combing museums and, 8 years later, find this tiny rock that, when they test it... seems to be a quasicrystal.
Luca had already sliced the mineral open to study its composition. He made six delicate sections, each the thickness of a human hair. In order to create the slices, though, Luca was forced to sacrifice the bulk of the sample. Ninety percent of what would eventually turn out to be an extremely precious mineral sample was destroyed in the process.
What a nightmare. The book gives a great overview of all of the nightmares that this sample destruction causes.
Another geologist, Hollister gets on board; he's so mean to everyone, so skeptical, but Paul, in classic trip report fashion, hints at this while playing it down hard, always tossing in nice notes about how welcome it was to have someone who wasn't a true believer.
The story is so good from here on out that I can't bear to summarize it, but here are a few more details of the detective story:
The sample that they almost destroyed was called "khatyrkite", and its origins are really uncertain. Luca (Paul's collaborator) and Paul spend hundreds of hours reading old geology notes, trying to track down the origins.
The Russian scientist who supposedly found it tries to elicit a huge bribe to give up the info about where he found it, at this tiny stream in the Kamchatka peninsula in Russia. As professors, Paul and his colleagues have no money, so they forget about it... but then, through a few other coincidences manage to track down the grad student who actually found the sample: Valery Kryachko. He's in his 50s now, but he's fired up and wants to take everyone back to the site to get more samples.
It just goes on and on, so much interesting geology, but the human story here is what's so great. I will say I have no idea what else is going on in Paul's life. He has a family, supposedly, and he's doing other work in physics, but he's comfortable to just keep this thing humming along.
Part III: Kamchatka Or Bust
This final section is too good to summarize really at all. The geologists convince Paul that to prove that natural quasicrystals exist, he needs to go to the Kamchatka peninsula, to this little bullshit stream, and get some more samples. I'm not sure Paul's ever been camping in his life; he tries to get out of actually going, but finally buckles and realizes that he's going to need to get after it. The Kamchatka peninsula turns out to be a hard-fucking-core first camping trip, no doubt about it.
Paul clearly had a lot of fun writing this piece, and was really proud. His son is a geologist and came along on the trip. And it just keeps getting better.
They go, they find the stream, dig everywhere, so much discovery, so much vodka. The team brings back huge amounts of material, and BOOM, they discover that the quasicrystal came from an asteroid, a previously undiscovered asteroid that slammed into the earth some untold number of years ago and carries insights into the origins of the solar system!
I'm excited and exhausted just writing about the journey. I can't imagine living it.
That's all I've got for now. Go get yourself a copy of "The Second Kind of Impossible" and revel in the detective tale that Paul's put together.

Comments
comments powered by Disqus